Introduction to Tree Data Structure

by · January 20, 2021

Tree Data Structure is a non-linear or hierarchical data structure. In terms of graph, tree data structure can be defined as a special type of graph data structure with no circuits in it.

General Tree
General Tree

Basic Terminologies of Tree Data Structure:

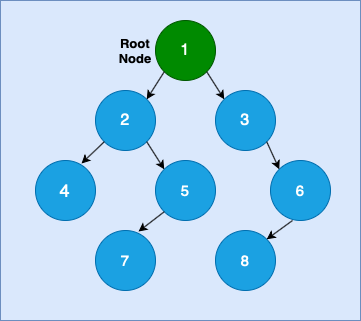
Root Node: Root Node is a first node in a tree from where tree originates. In any tree there is exactly one root node. In the following diagram, ‘1’ is a root node.

Root Node
Root Node in a Binary Tree

Edge: Edge is basically referred as connector between any two nodes of the tree. In a tree with ‘n’ number of nodes, there will always be exactly (n-1) number of edges.

Edge
Edge in a Binary Tree

Parent Node: A Parent Node is a node which has a directed branch from it to any other node. In general tree, parent node can have multiple children. 

General Tree

In the following diagram,

Node 1 is a parent node of Node 2 and Node 3.

Node 2 is a parent node of Node 4 and Node 5.

Node 3 is a parent node of Node 6.

Node 5 is a parent node of Node 7.

Node 6 is a parent node of Node 8.

Child Node: The Node which is descendant of some node is called Child Node. All the nodes in a tree except root node are child node. In general tree, a parent node can have multiple child nodes. In case of binary tree, which is special type of general tree, a parent node can have at most two child nodes.

General Tree

In the following diagram,

Node 2 and Node 3 are child Nodes of Node 1.

Node 4 and Node 5 are child Nodes of Node 2.

Node 6 is a child Node of Node 3.

Node 7 is a child Node of Node 5.

Node 8 is a child Node of Node 6.

Leaf Node: Leaf Node is a type of node in a tree which does not have any child nodes. In the following diagram, Node 4, Node 7 and Node 8 are Leaf Nodes of the Tree.

Leaf Node
Leaf Nodes

Sibling Nodes: Two nodes are known as sibling nodes of each other if they are directed from same parent node. In other words, sibling nodes have same ancestors.

Sibling Nodes
Sibling Nodes

Internal Node: Internal Nodes are those nodes which have at least one child node. In other words, internal nodes are non-leaf nodes. In the following diagram, Node 1, 2, 3, 5, 6 are internal nodes. 

Internal Nodes
Internal Nodes in a Binary Tree

Path: In a tree, the sequence of nodes and edges from one node to any other node is known as path. In the following diagram, the path from Node 1 to Node 7 is highlighted.

Path
Path in a Binary Tree

Degree of Node: Degree of node is defined as total number of immediate children of the node. In case of binary tree, the highest degree of any node is 2. 

General Tree

In the following diagram, 

The degree of Node 1 is 2.

The degree of Node 2 is 2.

The degree of Node 3 is 1.

The degree of Node 4 is 0.

The degree of Node 5 is 1.

The degree of Node 6 is 1.

The degree of Node 7 is 0.

The degree of Node 8 is 0.

Height/Depth of the Tree: The height of the tree is defined as total number of nodes in a longest path from root node to any leaf node. In the following diagram, the height of the tree is 4.

Path
Height Of Binary Tree

Level: The Level of the tree is defined as each step from root to bottom node(leaf) of the tree. The root node is present at level 0.

Level

Related Posts:

  1. Binary Tree Traversals
  2. Print All Leaf Nodes of a Binary Tree
  3. Count Number of Nodes in a Binary Tree
  4. Print Alternate Levels of Binary Tree
  5. Maximum Width of Binary Tree
  6. Level Order Tree Traversal
  7. Left View of Binary Tree
  8. Right View of Binary Tree
  9. Compute Height of Binary Tree
  10. Inorder Tree Traversal Using Stack
  11. Preorder Tree Trasversal Using Stack
  12. Postorder Tree Traversal Using Stack
  13. Vertical Order Tree Traversal
  14. Top View of Binary Tree
  15. Bottom View of Binary Tree
  16. Delete Complete Binary Tree
  17. Check if two trees are mirror Trees of Each Other
  18. Convert Binary Tree to its Mirror Tree
  19. Check if Binary Tree is Symmetric or Not
  20. Print All Root to Leaf Paths in a Binary Tree

You may also like...