Preorder Traversal of Binary Tree Using Stack

by · January 22, 2021

“Preorder Traversal of Binary Tree Using Stack” is an important traversal algorithm of tree data structure. Here, we are given a binary tree and our task is to traverse the given binary tree in preorder fashion using stack data structure.

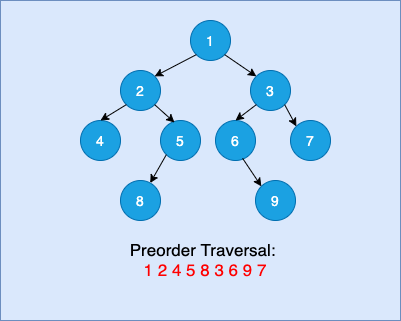
Preorder Traversal of Binary Tree Using Stack
Preorder Tree Traversal

Preorder Traversal:

  1. Visit Root Node and Print it.
  2. Visit Left Subtree
  3. Visit Right Subtree

We have already discussed recursive implementation here. Now, the iterative implementation of the same recursive solution will be discussed here.

The steps required to implement preorder traversal of Binary Tree Using Stack are as follows:

  1. Create an empty stack and push root node into it.
  2. Perform following operation until stack is not empty:
    1. Pop an element from stack and print it.
    2. Push Right Node, if exist, into the stack.
    3. Push Left Node, if exist, into the stack.

C++ Program to Implement Preorder traversal of Binary Tree Using Stack is as follows:

/* C++ Program to implement preorder traversal of binary tree using stack*/
#include<bits/stdc++.h>
using namespace std;

typedef struct Node
{
    int data;
    struct Node *left;
    struct Node *right;
    Node(int ele)
    {
        data = ele;
        left = NULL;
        right = NULL;
    }
} Node;

/* Function to implement Preorder Traversal */
void preorder(Node *root)
{
    /* Check Base Condition */
    if(root == NULL)
    return;
    
    /* Create an Empty Stack */
    stack <Node *> st;
    
    /* Push root Node into it */
    st.push(root);
    
    while(!st.empty())
    {
        /* Pop and print top node */
        Node *temp = st.top();
        st.pop();
        cout<<temp -> data<<" ";
        
        /* Push Right Child, if exists */
        if(temp -> right)
        st.push(temp -> right);
        
        /* Push Left Child, if exists */
        if(temp -> left)
        st.push(temp -> left);
    }
    
}

int main()
{
    /* Creating a Binary tree and inserting some nodes in it */
    Node *root = NULL;
    
    root = new Node(1);
    root -> left = new Node(2);
    root -> right = new Node(3);
    root -> left -> left = new Node(4);
    root -> left -> right = new Node(5);
    root -> right -> left = new Node(6);
    root -> right -> right = new Node (7);
    root -> left -> right -> left = new Node(8);
    root -> right -> left -> right = new Node(9);
    
    /* Calling function to perform preorder traversal*/
    cout<<"The Preorder Traversal of the Given Binary Tree is: ";
    preorder(root);
}

OUTPUT:

The Preorder Traversal of the Given Binary Tree is: 1 2 4 5 8 3 6 9 7

Related Posts:

  1. Inorder Tree Traversal Using Stack
  2. Postorder Tree Traversal Using Stack
  3. Vertical Order Tree Traversal
  4. Top View of Binary Tree
  5. Bottom View of Binary Tree
  6. Delete Complete Binary Tree
  7. Check if two trees are mirror Trees of Each Other
  8. Convert Binary Tree to its Mirror Tree
  9. Check if Binary Tree is Symmetric or Not
  10. Print All Root to Leaf Paths in a Binary Tree
  11. Introduction to Tree Data Structure
  12. Binary Tree Traversals
  13. Print All Leaf Nodes of a Binary Tree
  14. Count Number of Nodes in a Binary Tree
  15. Print Alternate Levels of Binary Tree
  16. Maximum Width of Binary Tree
  17. Level Order Tree Traversal
  18. Left View of Binary Tree
  19. Right View of Binary Tree
  20. Compute Height of Binary Tree

You may also like...