Largest Rectangular Area in Histogram
“Largest Rectangular Area in Histogram” is one of the favorite technical interview problem, asked in many product-based company interview.
Problem: We are given a histogram made up of contiguous bars of same width. Our task is to find the largest possible rectangular area.
Example:
Length of contiguous bars: {5, 7, 12, 2, 9, 8} . The largest possible area is 8*2 = 16.
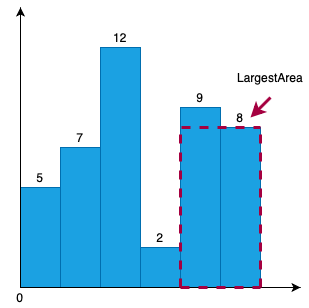
Largest Rectangular Area in Histogram
The length of contiguous bars will be provided as an Array.
This is a tricky question and can be solved using multiple approaches. Some of them are:
- Brute-Force Solution
- Stack Based Approach
METHOD 1: Brute-Force Approach
The simplest solution to find largest rectangular area would be to consider each bar as starting point and then calculate area considering that bar.
Set area = height[0]
Loop:
Set count = 1
Loop1.1:
Traverse all the previous bars(if exist) of that bar and check if the height of previous bar are greater than current starting bar or not. If the height of previous bar is greater than or equal to current(starting) bar, then increment count with 1 and continue to traverse to previous bars. If the height of previous bar is smaller than current(starting) bar, then break the loop.
Loop1.1 End
Loop1.2:
Similarly, traverse all the next bars(if exist) of that bar and check if the height of next bar are greater than current starting bar or not. If the height of next bar is greater than or equal to current(starting) bar, then increment count with 1 and continue to traverse to previous bars. If the height of previous bar is smaller than current(starting) bar, then break the loop.
Loop1.2 End
Calculate temp_area = height[i] * count;
If temp_area > area, then area = temp_area.
Loop End
The time complexity of brute force solution to find the largest rectangular area in histogram is O(n2).
C++ Program to find the largest rectangular area in histogram is as follows:
/* C++ Program to find largest rectangular area in histogram */
#include<bits/stdc++.h>
using namespace std;
/* Function to find largest rectangular area in histogram */
int findLargestArea(int hist[], int n)
{
int area = hist[0];
/*
Consider Each Bar as Starting Bar and Compute
Area using it.
*/
for(int i = 0; i < n; i++)
{
int count = 1;
/* Compute How many previous Bars(if exist) can be included in
computing Largest rectangular Area in Histogram
*/
for(int j = i-1; j >= 0; j--)
{
if(hist[j] >= hist[i])
count++;
else
break;
}
/* Compute How many Next Bars(if exist) can be included in
computing Largest rectangular Area in Histogram
*/
for(int j = i+1; j < n; j++)
{
if(hist[j] >= hist[i])
count++;
else
break;
}
int temp_area = hist[i] * count;
if(temp_area > area)
area = temp_area;
}
return area;
}
int main()
{
int hist[] = {5, 7, 12, 2, 9, 8};
int n = sizeof(hist)/sizeof(hist[0]);
int largest = findLargestArea(hist,n);
cout<<"The Largest Rectangular Histogram is "<<largest;
}
OUTPUT: The Largest Rectangular Area in Histogram is 16
METHOD 2: Stack Based Approach
The Stack Based Approach is much more time efficient than previous brute force approach. This Approach compute the “largest rectangular area in histogram” in O(n).
The steps required to compute largest rectangular area in histogram are as follows:
- Create an empty stack.
- Initialize max_area = 0.
- Start iterating the array, for every element of the array, push the index into the stack if the stack is empty or hist[i] >= hist[top stack element].
- When we encounter an element, hist[i] < hist[top stack element], keep popping element from our stack until we will find such element, hist[top stack element], which is smaller than or equal to current element(hist[i] >= hist[top stack element]) or stack is empty.
- Every time we popping element from our stack we will calculate square formed with these elements and store the result in temp_res.
- If temp_res > max_area, then max_area = temp_res.
- At last, keep popping remaining elements from stack and compute, compare and assign temp_res with max_area.
- Print the result.
C++ Program to find the largest rectangular area in histogram is as follows:
/* C++ Program to find largest rectangular area in histogram */
#include<bits/stdc++.h>
using namespace std;
int find_max_area(int hist[],int n)
{
/* Create Stack. Stack will hold indexes of hist[i] */
stack<int> st;
int curr_area; /*.To Hold Current Area */
int max_area=0; /* Resultant Variable */
int i=0;
while(i<n)
{
/*.If Stack is empty or current bar is greater than
stack top element, push the index into the stack */
if(st.empty() || hist[i]>=hist[st.top()])
st.push(i++);
else
{
/*
Else if the current element is smaller than stack top element,
Compute curr_area with stack elements until current element is
greater than equal to stack top element.
*/
int temp=st.top();
st.pop();
if(st.empty())
{
curr_area=hist[temp]*(i);
}
else
{
curr_area=hist[temp]*(i-st.top()-1);
}
/*.Update the max_area, if required */
if(curr_area>max_area)
{
max_area=curr_area;
}
}
}
/*.Now, Pop the remaining elements from stack and compute,
compare and assign max_area accordingly.
*/
while(!st.empty())
{
int temp=st.top();
st.pop();
if(st.empty())
{
curr_area=hist[temp]*(i);
}
else
{
curr_area=hist[temp]*(i-st.top()-1);
}
if(curr_area>max_area)
{
max_area=curr_area;
}
}
return max_area;
}
int main()
{
int hist[] = {5, 7, 12, 2, 9, 8};
int n = sizeof(hist)/sizeof(hist[0]);
int area=find_max_area(hist,n);
cout<<"The largest rectangular area in histogram is "<<area<<"\n";
}
OUTPUT: The largest rectangular area in histogram is 16
Related Posts:
- Length of Longest Valid Substring
- Reverse a String using Stack
- Implement two stacks in a single array
- Print Bracket Number
- Next Greater Frequency Element
- Sort a Stack using Temporary Stack
- Infix to Postfix Conversion
- Infix to Prefix Conversion
- Prefix to Infix Conversion
- Prefix to Postfix Conversion
- Postfix to Infix Conversion
- Postfix to Prefix Conversion
- Check whether given Parentheses String are Balanced Parentheses or Not.
- Next Greater Element
- Find Minimum number of bracket reversals required to make an expression balanced.
- Implement Queue Using Two Stacks.
- Merge Overlapping Intervals using Stacks
- Implement Stack Using Linked List
- Find First Non-Repeating Character of the String.
- Find Most Frequent Element of the Array.


