Inorder Tree Traversal Using Stack

by · January 22, 2021

“Inorder Tree Traversal Using Stack” is a binary tree traversal algorithm where we traverse the given tree in inorder fashion using stack data structure. 

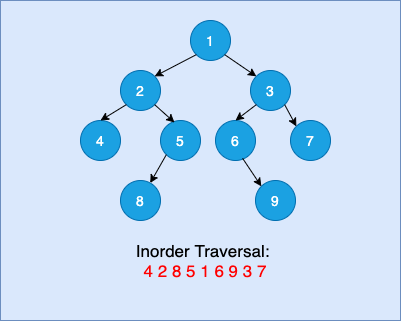
Inorder Tree Traversal Using Stack
Inorder Tree Traversal

We have already discussed the recursive approach of the inorder traversal. Here, we implement the same algorithm using stack data structure.

The steps required to implement inorder tree traversal using stack data structure are as follows:

  1. Create an Empty Stack “st” of Node Type.
  2. Initialize currNode = Root Node.
  3. Loop until currNode is not empty or stack is not empty:
    1. Using Loop, set currNode = currNode -> left until current is NULL.
    2. Assign currNode = st.top()
    3. Pop out top node of stack
    4. Print “currNode -> data”
    5. Assign currNode = currNode -> Right.

C++ Program to implement Inorder Tree Traversal Using Stack is as follows:

/* C++ Program to implement inorder tree traversal using stack*/
#include<bits/stdc++.h>
using namespace std;

typedef struct Node
{
    int data;
    struct Node *left;
    struct Node *right;
    Node(int ele)
    {
        data = ele;
        left = NULL;
        right = NULL;
    }
} Node;

/* Function to Implement inorder traversal */
void inorder(Node *root)
{
    /* Check Base Condition */
    if(root == NULL)
    return;
    
    /* Create an Empty Stack */
    stack <Node *> st;
    
    Node *currNode = root;
    
    while(currNode != NULL || !st.empty())
    {
        /* Reach the left most node of the tree */
        while(currNode)
        {
            st.push(currNode);
            currNode = currNode -> left;
        }
        
        /* Assign Left to Left most node */
        currNode = st.top();
        
        /* Pop out the stack */
        st.pop();
        
        /* Print currNode data */
        cout<<currNode -> data <<" ";
        
        /* Traverse right Subtree */
        currNode = currNode -> right;
    }
    
}

int main()
{
    /* Creating a Binary tree and inserting some nodes in it */
    Node *root = NULL;
    
    root = new Node(1);
    root -> left = new Node(2);
    root -> right = new Node(3);
    root -> left -> left = new Node(4);
    root -> left -> right = new Node(5);
    root -> right -> left = new Node(6);
    root -> right -> right = new Node (7);
    root -> left -> right -> left = new Node(8);
    root -> right -> left -> right = new Node(9);
    
    /* Calling function to perform inorder traversal*/
    cout<<"The Inorder Traversal of the Given Binary Tree is: ";
    inorder(root);
}

OUTPUT:

The Inorder Traversal of the Given Binary Tree is: 4 2 8 5 1 6 9 3 7

Related Posts:

  1. Preorder Tree Trasversal Using Stack
  2. Postorder Tree Traversal Using Stack
  3. Vertical Order Tree Traversal
  4. Top View of Binary Tree
  5. Bottom View of Binary Tree
  6. Delete Complete Binary Tree
  7. Check if two trees are mirror Trees of Each Other
  8. Convert Binary Tree to its Mirror Tree
  9. Check if Binary Tree is Symmetric or Not
  10. Print All Root to Leaf Paths in a Binary Tree
  11. Introduction to Tree Data Structure
  12. Binary Tree Traversals
  13. Print All Leaf Nodes of a Binary Tree
  14. Count Number of Nodes in a Binary Tree
  15. Print Alternate Levels of Binary Tree
  16. Maximum Width of Binary Tree
  17. Level Order Tree Traversal
  18. Left View of Binary Tree
  19. Right View of Binary Tree
  20. Compute Height of Binary Tree

You may also like...