Print all Root to Leaf Paths in a Binary Tree
“Print all Root to Leaf Paths in a Binary Tree” is an important algorithmic problem based on tree data. Here, we are given a binary tree and our task is to write a program to print all root to leaf paths in given binary tree.
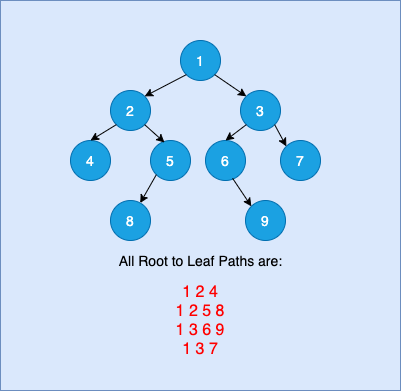
Here, the idea is to traverse the given binary tree in preorder fashion and push every encountered node in current path from root to leaf in a vector.
If encountered node is leaf node, we will print the whole vector.
After that, pop out current node from vector after left and right subtree are traversed.
C++ Program to print all root to leaf paths in a binary tree is as follows:
/* C++ Program to Print All Root to Leaf Path in a Binary Tree */
#include<bits/stdc++.h>
using namespace std;
typedef struct Node
{
int data;
struct Node *left;
struct Node *right;
Node(int ele)
{
data = ele;
left = NULL;
right = NULL;
}
} Node;
/* Function to Print All Root to Leaf Path in a Binary Tree */
void printPaths(Node *root, vector<int> &vc)
{
/* Base Condition: Empty Tree */
if(root == NULL)
return;
/* Push Node in current Path Vector */
vc.push_back(root -> data);
/* If current Node is Leaf Node, we'll print the Path */
if(root -> left == NULL && root -> right == NULL)
{
for(int i = 0; i < vc.size(); i++)
cout<<vc[i]<<" ";
cout<<endl;
}
/* Recur for Left and Right Subtree */
printPaths(root -> left, vc);
printPaths(root -> right, vc);
/* Pop Out Current Node after left and right subtree are done */
vc.pop_back();
}
/* Function to Print All Root to Leaf Path in a Binary Tree */
void printRootToLeaf(Node *root)
{
/* Base Condition: Empty Tree */
if(root == NULL)
return;
vector<int> vc;
printPaths(root,vc);
}
int main()
{
/* Creating a Binary trees and inserting some nodes in it */
Node *root = NULL;
root = new Node(1);
root -> left = new Node(2);
root -> right = new Node(3);
root -> left -> left = new Node(4);
root -> left -> right = new Node(5);
root -> right -> left = new Node(6);
root -> right -> right = new Node (7);
root -> left -> right -> left = new Node(8);
root -> right -> left -> right = new Node(9);
/* Calling function to Print All Root to Leaf Path in a Binary Tree */
printRootToLeaf(root);
}
OUTPUT:
1 2 4 1 2 5 8 1 3 6 9 1 3 7
Related Posts:
- Introduction to Tree Data Structure
- Binary Tree Traversals
- Print All Leaf Nodes of a Binary Tree
- Count Number of Nodes in a Binary Tree
- Print Alternate Levels of Binary Tree
- Maximum Width of Binary Tree
- Level Order Tree Traversal
- Left View of Binary Tree
- Right View of Binary Tree
- Compute Height of Binary Tree
- Inorder Tree Traversal Using Stack
- Preorder Tree Trasversal Using Stack
- Postorder Tree Traversal Using Stack
- Vertical Order Tree Traversal
- Top View of Binary Tree
- Bottom View of Binary Tree
- Delete Complete Binary Tree
- Check if two trees are mirror Trees of Each Other
- Convert Binary Tree to its Mirror Tree
- Check if Binary Tree is Symmetric or Not


