Bottom View of Binary Tree
“Bottom View of Binary Tree” is one of the foremost algorithmic problem asked in technical interviews of product-based companies. Here, we are given a binary tree and our task is to write a program to print the bottom view of given binary tree.
Bottom View of Binary Tree is referred to those nodes of binary tree which can be seen from bottom of the tree.
We need to print the node values from left to right.
If there are multiple bottom-most nodes for a same horizontal distance from root node, then we need to print the one which occurs later in our traversal algorithm.
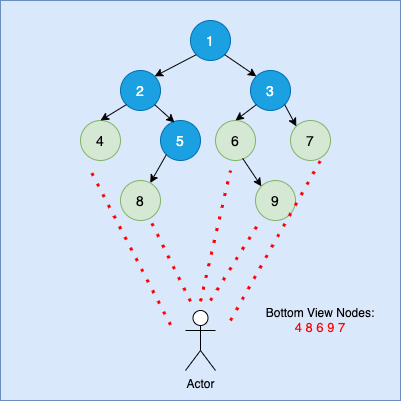
The idea here is similar to vertical order traversal of binary tree. We will perform the vertical order traversal and print only those nodes which occurs in last of vertical order line.
The steps required to print bottom view of binary tree are as follows:
- Create a map which store the vertical order line number and corresponding bottom node value.
- Create a queue which can accommodate both node and corresponding horizontal distance with root node.
- Insert the root node into queue and 0 as horizontal distance.
- Perform following steps until queue is node empty.
- Pop front Element of queue.
- Assign the popped node value to map, according to horizontal distance. Every time we encounter a node with already existing horizontal distance node value present in the map, we will replace it.
- If left child exists of popped node, insert into queue with horizontal distance as current HD-1.
- If right child exists of popped node, insert into queue with horizontal distance as current HD+1.
- Print the map data which contains bottom view.
C++ Program to print bottom view of binary tree are as follows:
/* C++ Program to print Bottom View of Binary Tree */
#include<bits/stdc++.h>
using namespace std;
typedef struct Node
{
int data;
struct Node *left;
struct Node *right;
Node(int ele)
{
data = ele;
left = NULL;
right = NULL;
}
} Node;
/* Function to print bottom view of Binary Tree */
void bottomView(Node *root)
{
/* Base Case */
if(root == NULL)
return;
/*
Create a map which store bottom view nodes
key: vertical order line
Value: Top node of vertical order line
*/
map<int, int> mp;
/*
Create queue which store both node and corresponding HD
*/
queue<pair<Node*, int>> que;
int hd = 0;
que.push(make_pair(root,hd));
while(!que.empty())
{
/* Pop front Node */
pair<Node *,int> temp = que.front();
que.pop();
Node *temp_node = temp.first;
int currHD = temp.second;
/*
Assign the popped node value to map having same HD.
Every time we find a node having same horizontal distance,
we replace its value in the map
*/
mp[currHD] = temp_node -> data;
if(temp_node -> left)
que.push(make_pair(temp_node -> left, currHD - 1));
if(temp_node -> right)
que.push(make_pair(temp_node -> right, currHD + 1));
}
/* Print map, which contain bottom view nodes */
map<int, int> :: iterator itr;
for(itr = mp.begin(); itr != mp.end(); ++itr)
{
cout << itr -> second << " ";
}
}
int main()
{
/* Creating a Binary tree and inserting some nodes in it */
Node *root = NULL;
root = new Node(1);
root -> left = new Node(2);
root -> right = new Node(3);
root -> left -> left = new Node(4);
root -> left -> right = new Node(5);
root -> right -> left = new Node(6);
root -> right -> right = new Node (7);
root -> left -> right -> left = new Node(8);
root -> right -> left -> right = new Node(9);
/* Calling function to print bottom view of binary tree*/
cout<<"The bottom View of Given Binary Tree is:\n";
bottomView(root);
}
OUTPUT:
The bottom View of Given Binary Tree is: 4 8 6 9 7
Related Posts:
- Top View of Binary Tree
- Introduction to Tree Data Structure
- Binary Tree Traversals
- Print All Leaf Nodes of a Binary Tree
- Count Number of Nodes in a Binary Tree
- Print Alternate Levels of Binary Tree
- Maximum Width of Binary Tree
- Level Order Tree Traversal
- Left View of Binary Tree
- Right View of Binary Tree
- Compute Height of Binary Tree
- Inorder Tree Traversal Using Stack
- Preorder Tree Trasversal Using Stack
- Postorder Tree Traversal Using Stack
- Vertical Order Tree Traversal
- Delete Complete Binary Tree
- Check if two trees are mirror Trees of Each Other
- Convert Binary Tree to its Mirror Tree
- Check if Binary Tree is Symmetric or Not
- Print All Root to Leaf Paths in a Binary Tree


