Check if two trees are mirror tree of each other

“Check if two trees are mirror tree of each other” is a basic problem based on tree data structure. Here, we are given two binary tree and our task is to write a program to check whether given two binary trees are mirror tree of each other.

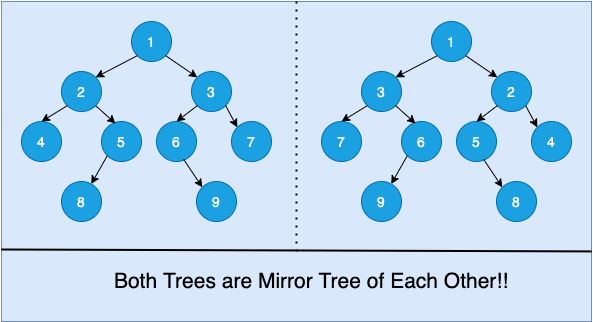
Two trees are known as mirror tree of each other if they satisfy following conditions:

1. Both must be empty or non-empty tree.
2. Root Node data must be same.
3. Left subtree of first tree must be equal to right subtree of second tree.
4. Right subtree of first tree must be equal to left subtree of second tree.

C++ Program to check if two trees are mirror tree of each other is as follows:

/* C++ Program to check if two trees are mirror tree of each other */
#include<bits/stdc++.h>
using namespace std;

typedef struct Node
{
    int data;
    struct Node *left;
    struct Node *right;
    Node(int ele)
    {
        data = ele;
        left = NULL;
        right = NULL;
    }
} Node;

/* Function to check if two trees are mirror tree of each other */
bool checkMirror(Node *root1, Node *root2)
{
    /* Base Case1: If both Trees are Empty */
    if(root1 == NULL && root2 == NULL)
    return true;
    
    /* Base Case2: If one tree is empty and other not */
    if(root1 == NULL || root2 == NULL)
    return false;
    
    /*
        If Both are Non-Empty, Recursively compare data of left subtree of 
        first tree with right subtree of second tree and vice-versa
    */
    return root1 -> data == root2 -> data &&
           checkMirror(root1 -> left, root2 -> right) &&
           checkMirror(root1 -> right,root2 -> left);
}

int main()
{
    /* Creating a Binary trees and inserting some nodes in it */
    Node *root1 = NULL;
    Node *root2 = NULL;
    
    /* Inserting some Nodes in first tree */
    root1 = new Node(1);
    root1 -> left = new Node(2);
    root1 -> right = new Node(3);
    root1 -> left -> left = new Node(4);
    root1 -> left -> right = new Node(5);
    root1 -> right -> left = new Node(6);
    root1 -> right -> right = new Node (7);
    root1 -> left -> right -> left = new Node(8);
    root1 -> right -> left -> right = new Node(9);
    
    /* Inserting some Nodes in second tree */
    root2 = new Node(1);
    root2 -> right = new Node(2);
    root2 -> left = new Node(3);
    root2 -> right -> right = new Node(4);
    root2 -> right -> left = new Node(5);
    root2 -> left -> right = new Node(6);
    root2 -> left -> left = new Node (7);
    root2 -> right -> left -> right = new Node(8);
    root2 -> left -> right -> left = new Node(9);
    
    /* Calling function to check if two trees are mirror tree of each other*/
    if(checkMirror(root1,root2) == true)
    {
        cout<<"Both Trees are Mirror Tree of Each Other!!";
    }
    else
    {
        cout<<"Both Trees are not Mirror Tree of Each Other!!";
    }
    
}

OUTPUT:

Both Trees are Mirror Tree of Each Other!!

---

Related Posts:

1. Convert Binary Tree to its Mirror Tree
2. Check if Binary Tree is Symmetric or Not
3. Print All Root to Leaf Paths in a Binary Tree
4. Introduction to Tree Data Structure
5. Binary Tree Traversals
6. Print All Leaf Nodes of a Binary Tree
7. Count Number of Nodes in a Binary Tree
8. Print Alternate Levels of Binary Tree
9. Maximum Width of Binary Tree
10. Level Order Tree Traversal
11. Left View of Binary Tree
12. Right View of Binary Tree
13. Compute Height of Binary Tree
14. Inorder Tree Traversal Using Stack
15. Preorder Tree Trasversal Using Stack
16. Postorder Tree Traversal Using Stack
17. Vertical Order Tree Traversal
18. Top View of Binary Tree
19. Bottom View of Binary Tree
20. Delete Complete Binary Tree

---