Infix to Postfix Conversion
“Infix to postfix conversion” is a classic example of stack data structure. Stack can be used to convert given infix expression to corresponding postfix expression.
Operator: Operator are symbols that instruct the computer to perform simple and single tasks. Examples of operators includes + (Addition), – (Subtraction), * (multiplication),… and many more.
Operand: Operands are values or variable on which operator works its tasks. Examples of Operand includes “a”, “b”, 23, 12,.. and many more.
Steps to convert infix to postfix expression
- Scan the valid infix expression from left to right.
- Initialize the empty character stack and empty postfix string.
- If the scanned character is an operand, add it to postfix string.
- If the scanned character is open parenthesis, push it to the stack.
- If the scanned character is closing parenthesis, pop all the characters of the stack and concatenate to the end of the postfix string until opening parenthesis occurs.
- Pop the open parenthesis.
- If the scanned character is an Operator and the stack is not empty, compare the precedence of the character with the element on top of the stack. If top element of the Stack has higher precedence over the scanned character, pop the stack else push the scanned character to stack. Repeat this step until the stack is not empty and top Stack has precedence over the character.
- Repeat steps 3 to 7 until all characters are scanned.
- If the stack is empty, return the postfix string.
- Else, pop the elements of the stack and add it to postfix string, and then return the postfix string.
Example (Infix to Postfix Conversion)
Suppose, we want to convert the following infix expression to postfix expression:
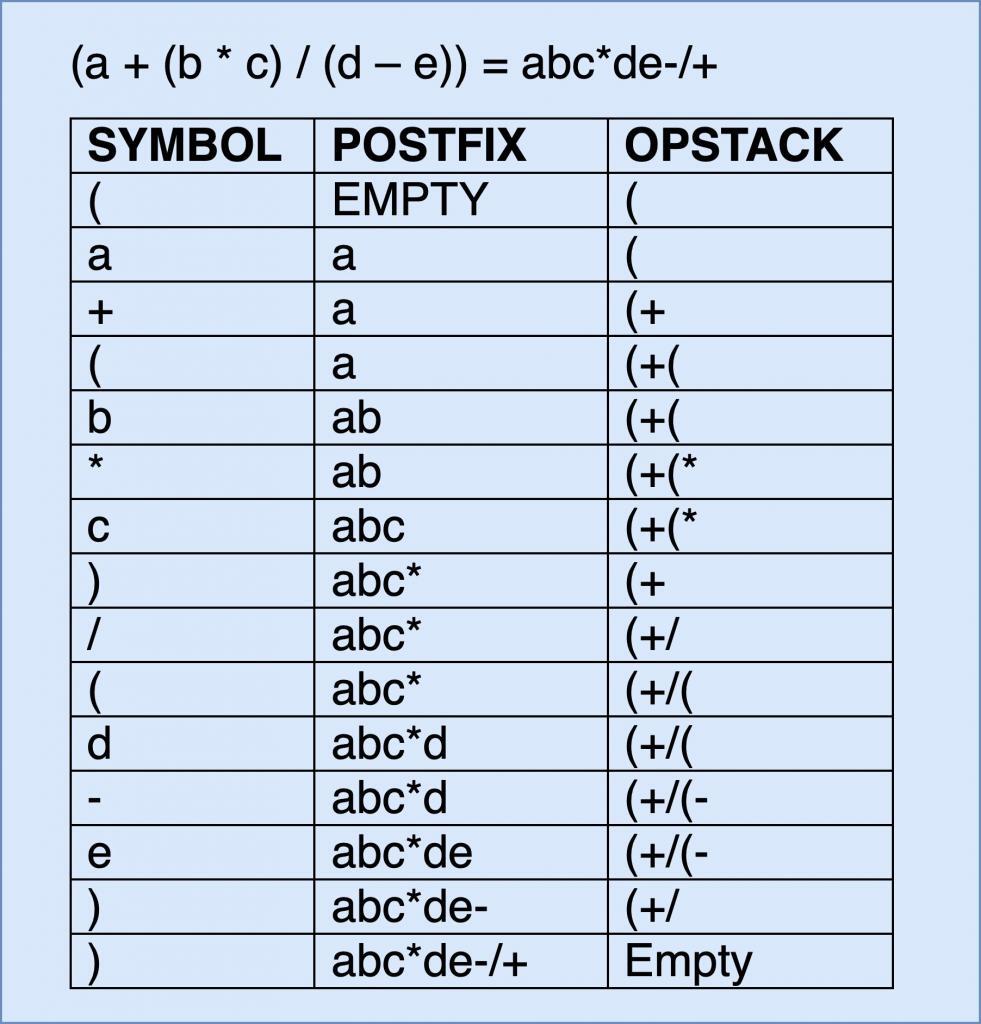
Infix to Postfix
Algorithm for converting infix to postfix expression
Algo infix_to_postfix (infix)
{
// input- valid infix expression.
// output- corresponding postfix expression.
1.i= 0;
2.Loop(i<sizeof(infix))
{
1.If(infix[i] == ‘(’ )
Then push infix[i] into stack.
2.Else if(infix[i] == ‘)‘ )
{
a.Token = popstack();
b.Loop (Token! = ‘(’ )
{
Concatenate Token to prefix string.
Token = popstack ();
}
}
3.Else if(infix[i] is an operator)
{
Ch=peep ();
Loop (stack not empty AND Priority (infix[i]) <=priority (Ch))
{
Ch=popstack ();
Concatenate ch to postfix string
Ch=peep ();
}
push infix[i] into stack.
}
4.Else if(infix[i] is an operand)
Then push infix[i] into stack.
}
3.Loop(stack not empty)
{
Ch=popstack ();
Concatenate ch to postfix string.
}
4.Print the postfix string in reverse order.
}// End.
C++ Program for converting infix to postfix expression is as follows:
/* C++ Program for infix to postfix conversion */
#include<iostream>
#include<string>
using namespace std;
class stack
{
string item;
int top;
public:
stack()
{
top=-1;
}
void push(char ch)
{
top++;
item[top]=ch;
}
char pop()
{
if(isempty())
{
cout<<"stack underflow!!";
return '@';
}
int ele;
ele=item[top];
top--;
return ele;
}
int isempty()
{
if(top==-1)
return 1;
return 0;
}
char peep()
{
return(item[top]);
}
int priority(char ch)
{
if(ch=='(')
return 1;
else if(ch=='+' || ch=='-')
return 2;
else if(ch=='*' || ch=='/' || ch=='%')
return 3;
else
return 4;
}
};
int main()
{
string infix,postfix;
char token,token_out,ch2,ch;
int i,len;
stack st;
cout<<"Enter the infix expression: ";
cin>>infix;
len=infix.size();
for(i=0;i<len;i++)
{
token=infix[i];
// If open parenthesis occurs, Push it into stack
if(token=='(')
{
st.push(token);
}
/* If Closing parenthesis occurs,
Pop the stack until Open parenthesis occurs*/
else if(token==')')
{
token_out=st.pop();
while(token_out!='(')
{
postfix.push_back(token_out);
token_out=st.pop();
}
}
// If character is operator
else if(infix[i]=='+' || infix[i]=='-' || infix[i]=='*' || infix[i]=='/' || infix[i]=='^')
{
ch2=st.peep();
while( !st.isempty() && st.priority(infix[i])<=st.priority(ch2))
{
ch=st.pop();
postfix.push_back(ch);
ch2=st.peep();
}
st.push(infix[i]);
}
// If character is operand, push it into stack
else
st.push(infix[i]);
}
/*Empty the stack and concatenate
the character to output String */
while(!st.isempty())
{
ch=st.pop();
postfix.push_back(ch);
}
cout<<"Postfix Expression: "<<postfix<<"\n";
return 0;
}
OUTPUT: Enter the infix expression: (a+(b*c)/(d-e)) Postfix Expression: abc*de-/+
Related Posts:
- Infix to Prefix Conversion
- Prefix to Infix Conversion
- Prefix to Postfix Conversion
- Postfix to Infix Conversion
- Postfix to Prefix Conversion
- Check whether given Parentheses String are Balanced Parentheses or Not.
- Next Greater Element
- Find Minimum number of bracket reversals required to make an expression balanced.
- Implement Queue Using Two Stacks.
- Swap Adjacent Elements of the Linked List.
- Count All Occurrences of a Particular Node in a Linked List.
- Merge Overlapping Intervals using Stacks
- Implement Stack Using Linked List
- Largest Rectangular Area in Histogram
- Length of Longest Valid Substring
- Reverse a String using Stack
- Implement two stacks in a single array
- Print Bracket Number
- Next Greater Frequency Element
- Sort a Stack using Temporary Stack


