Print Matrix in zig-zag order
“Print Matrix in zig-zag order” is a a problem of printing the given matrix of size N*M in zig-zag order.
The zig-zag order of the matrix is traversing the first row of matrix from left to right, next row from right to left, next row from left to right and so on.
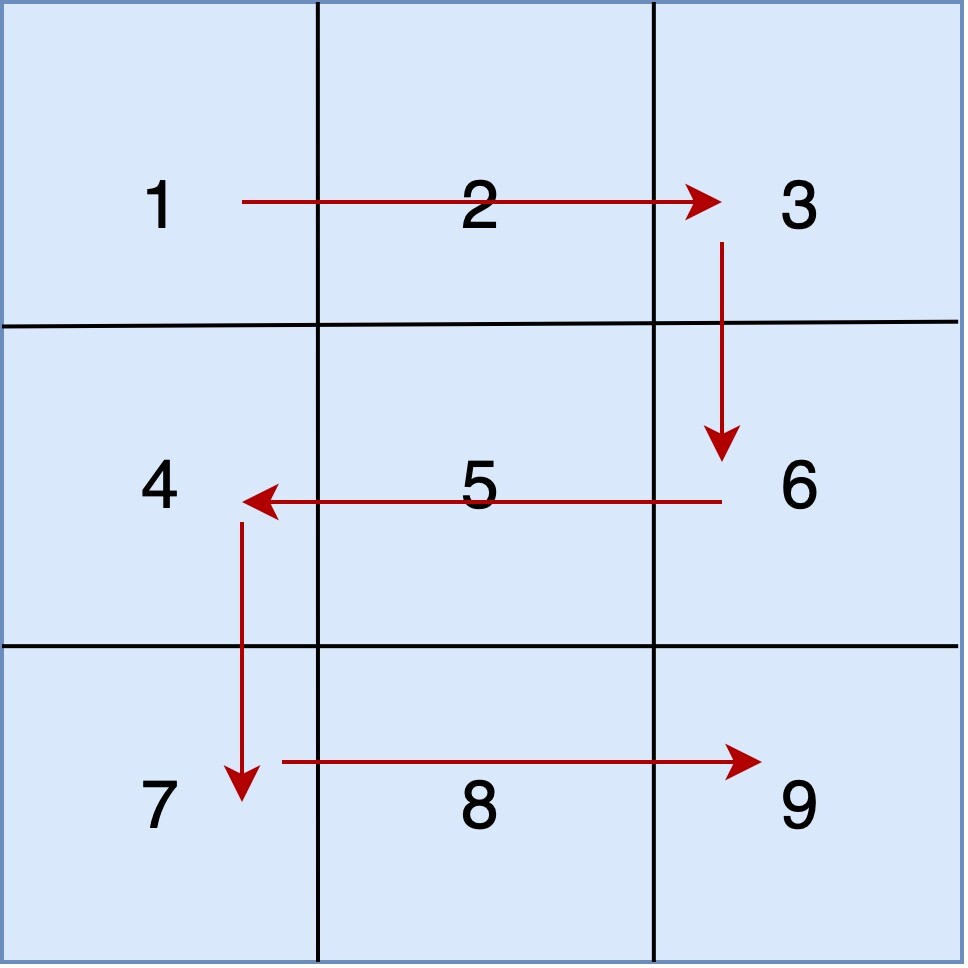
Print Matrix in Zig-Zag Order
Example:
Input: 1 2 3 4 5 6 7 8 9 OUTPUT: 1 2 3 6 5 4 7 8 9
C++ Program to Print matrix in Zig-Zag Order is as follows:
/* Program to Print matrix in Zig-Zag Order */
#include<bits/stdc++.h>
using namespace std;
int main()
{
int N,M;
// Scan Dimensions of the matrix
cout<<"Enter the dimension of the matrix:\n";
cin>>N>>M;
int matrix[N][M];
// Scan Matrix Elements
cout<<"Enter the elements of the matrix:\n";
for(int i = 0 ; i < N ; i++)
for(int j = 0 ; j < M ; j++)
cin>>matrix[i][j];
// Print the matrix in Zig-Zag Order
cout<<"The Zig-zag traversal of the matrix is:\n";
for(int i = 0 ; i < N ; i++)
{
if(i%2==0)
{
for(int j = 0 ; j < M ; j++)
cout<<matrix[i][j]<<" ";
}
else
{
for(int j = M-1 ; j>=0 ; j--)
cout<<matrix[i][j]<<" ";
}
}
}
OUTPUT: Enter the dimension of the matrix: 3 3 Enter the elements of the matrix: 1 2 3 4 5 6 7 8 9 The Zig-zag traversal of the matrix is: 1 2 3 6 5 4 7 8 9
Related Posts:
- Program to print matrix in spiral order.
- Program to sort a matrix.
- Program to Add two Matrix.
- Program to Transpose a Matrix.
- Program to Multiply Two Matrix.
- Program to check Identity Matrix.
- Program to check Idempotent Matrix.
- Program to check Involuntary Matrix.
- Program to find Power of the Number.
- Program to find Quotient and Remainder.
- Program to find largest amongst three numbers.
- Program to find factorial of a number.
- Program to find GCD of two numbers.
- Program to find LCM of two numbers.
- Program to check whether entered number is odd or even.
- Program to check whether entered number is prime number or not.
- Program to check whether entered number is palindrome or not.
- Program to check whether entered number is Armstrong Number or Not.
- Program to convert binary number to octal number.
- Program to convert binary number to decimal number.


