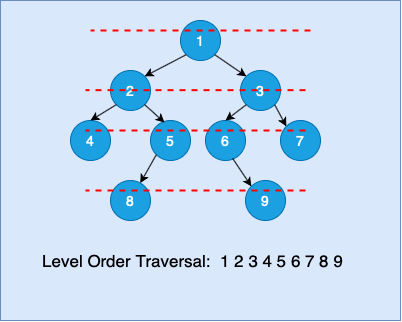
Level Order Tree Traversal

by · January 21, 2021

Level Order Tree Traversal or Breadth First Traversal is another type of tree traversal algorithm where we traverse all nodes of the binary tree level-by-level.

In previous post, we have already discussed preorder, inorder and postorder tree traversals which are typical types of Depth First Traversals. Trees can be traversed in level manner also, where all the nodes of first level are traversed and printed, then all nodes of second level are traversed and printed and in the same manner all the nodes of all levels are traversed and printed.

Level Order Tree Traversal
Level Order Tree Traversal

There are basically two approach to implement level order tree traversal:

  1. Brute-Force Approach
  2. Queue Based Approach

METHOD 1: Brute-Force Approach

The simplest solution to implement level order tree traversal is to traverse and print the nodes at level 1, then traverse and print the nodes at level 2 and so on; till all the nodes of every level are not traversed and printed.

All the nodes at every level can be printed using modifying pre-order traversal algorithm.

C++ Program to Implement Level Order Tree Traversal is as follows:

/* C++ Program to Implement Level Order Tree Traversal*/
#include<bits/stdc++.h>
using namespace std;

typedef struct Node
{
    int data;
    struct Node *left;
    struct Node *right;
    Node(int ele)
    {
        data = ele;
        left = NULL;
        right = NULL;
    }
} Node;


/* Function to Compute height of a Binary Tree */
int height(Node *root)
{
    /* If tree is empty, height will be 0 */
    if(root == NULL)
    {
        return 0;
    }
    else
    {
        /* Compute Height of Left Subtree */
        int leftHeight = height(root -> left);
        
        /* Compute Height of Right Subtree */
        int rightHeight = height(root -> right);
        
        /* Return max of height of subtree and right subtree + 1 */
        return max(leftHeight,rightHeight) + 1;
    }
}

/* Function to Print Nodes of a Particular Level */
void printLevel(Node *root, int level)
{
    if(root == NULL)
    return;
    
    if(level == 1)
    cout<<root -> data<< " ";
    else if(level > 1)
    {
        printLevel(root -> left,level-1);
        printLevel(root -> right, level-1);
    }
}

/* Function to count number of nodes in a Binary Tree */
void levelOrder(Node *root)
{
    /* Basic Test Case Scenerio */
    if(root == NULL)
    return;
    
    /* Compute Height and print Level by Level */
    int h = height(root);
    for(int i = 1; i <= h; i++)
    printLevel(root,i);
}

int main()
{
    /* Creating a Binary tree and inserting some nodes in it */
    Node *root = NULL;
    
    root = new Node(1);
    root -> left = new Node(2);
    root -> right = new Node(3);
    root -> left -> left = new Node(4);
    root -> left -> right = new Node(5);
    root -> right -> left = new Node(6);
    root -> right -> right = new Node (7);
    root -> left -> right -> left = new Node(8);
    root -> right -> left -> right = new Node(9);
    
    /* Calling function for Level Order Traversal */
    cout<<"The Level Order Traversal of the Given Binary Tree is:\n";
    levelOrder(root);
}

OUTPUT:

The Level Order Traversal of the Given Binary Tree is:
1 2 3 4 5 6 7 8 9

METHOD 2: Queue Based Approach

The steps required to traverse a binary tree using level order traversal are as follows:

  1. Create a queue and push root node in it.
  2. Until queue is not empty, perform following steps:
    1. Print the front node of the queue.
    2. If front node has left child, then, push it into queue.
    3. If front node has right child, then, push it into queue.
    4. Pop out the front node.

C++ Program to Implement Level Order Tree Traversal is as follows:

/* C++ Program to Implement Level Order Tree Traversal */
#include<bits/stdc++.h>
using namespace std;

typedef struct Node
{
    int data;
    struct Node *left;
    struct Node *right;
    Node(int ele)
    {
        data = ele;
        left = NULL;
        right = NULL;
    }
} Node;

/* Function to implement level order traversal */
void levelOrder(Node *root)
{
    /* Basic Test Case Scenerio */
    if(root == NULL)
    return;
    
    queue <Node*> qu;
    
    qu.push(root);
    
    while(!qu.empty())
    {
        Node *temp = qu.front();
        cout<<temp -> data<<" ";
       
        if(qu.front() -> left)
        qu.push(qu.front() -> left);
        
        if(qu.front() -> right)
        qu.push(qu.front() -> right);
       
        qu.pop();
    }
}

int main()
{
    /* Creating a Binary tree and inserting some nodes in it */
    Node *root = NULL;
    
    root = new Node(1);
    root -> left = new Node(2);
    root -> right = new Node(3);
    root -> left -> left = new Node(4);
    root -> left -> right = new Node(5);
    root -> right -> left = new Node(6);
    root -> right -> right = new Node (7);
    root -> left -> right -> left = new Node(8);
    root -> right -> left -> right = new Node(9);
    
    /* Calling function for Level Order Traversal */
    cout<<"The Level Order Traversal of the Given Binary Tree is:\n";
    levelOrder(root);
}

OUTPUT:

The Level Order Traversal of the Given Binary Tree is:
1 2 3 4 5 6 7 8 9

Related Posts:

  1. Introduction to Tree Data Structure
  2. Binary Tree Traversals
  3. Print All Leaf Nodes of a Binary Tree
  4. Count Number of Nodes in a Binary Tree
  5. Print Alternate Levels of Binary Tree
  6. Maximum Width of Binary Tree
  7. Left View of Binary Tree
  8. Right View of Binary Tree
  9. Compute Height of Binary Tree
  10. Inorder Tree Traversal Using Stack
  11. Preorder Tree Trasversal Using Stack
  12. Postorder Tree Traversal Using Stack
  13. Vertical Order Tree Traversal
  14. Top View of Binary Tree
  15. Bottom View of Binary Tree
  16. Delete Complete Binary Tree
  17. Check if two trees are mirror Trees of Each Other
  18. Convert Binary Tree to its Mirror Tree
  19. Check if Binary Tree is Symmetric or Not
  20. Print All Root to Leaf Paths in a Binary Tree

You may also like...