Stock Span Problem

“Stock Span Problem” is a classic problem of stack data structure, asked in technical interviews of many product-based companies. Here, we are given a price of a single stock for ‘N’ consecutive days and our task is to find the stock span for each day.

Stock Span is defined as number of consecutive days prior to current day when the price of a stock was less than or equal to the price at current day.

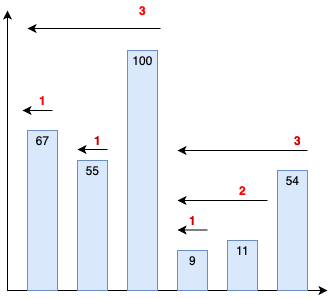
Example:
 
Let’s assume the price of single stock for ‘N’ consecutive days is:
{67, 55, 100, 9, 11, 54}
The stock span would be:
{1, 1, 3, 1, 2, 3}
 
Explanation: 
 
Day 1: 
Stock Price = 67
As, it is first day, the stock span would be 1.
 
Day 2:
Stock Price = 55
Stock price on previous day is 67 which is greater than 55, so we halt the loop and the stock span for day 2 would be 1.
 
Day 3:
Stock Price = 100
Stock price on previous day is 55 which is smaller than 100, so we increment the stock pan by 1, then we continue the loop and go to previous day which is day 1 with stock price 67, which is also smaller than 100, so again, we increment the stock span by 1. 
Finally, for day 3, the stock span would be 3.
 
Day 4:
Stock Price = 9
Stock price on previous day is 100 which is greater than 9, so we halt the loop and the stock span for day 4 would be 1.
 
Day 5:
Stock Price = 11
Stock price on previous day is 9 which is smaller than 11, so we increment the stock pan by 1, then we continue the loop and go to previous day, which is day 3 with stock price 100, which is greater than 11, so, we halt the loop.
Finally, for day 5, the stock span would be 2.
 
Day 6:
Stock Price = 54
Stock price on previous day is 11 which is smaller than 54, so we increment the stock pan by 1, then we continue the loop and go to previous day, which is day 4 with stock price 9, which is also smaller than 54, so again, we increment the stock span by 1. Then, we continue the loop and go to previous day, which is day 3 with stock price 100, which is greater than 54. So, we halt the loop. 
Finally, for day 6, the stock span would be 3.

There are basically two methods to solve stock span problem. These are:

1. Brute-Force Approach
2. Stack Based Approach

Method 1: Brute-Force Approach

The simplest method to solve stock span problem is that, for every stock price, traverse the previous days of stock price and increment the span value of it while stock price on previous day are smaller or equal to current day stock price.

C++ Program to implement stock span problem is as follows:

/* C++ Problem to implement stock span problem */
#include<bits/stdc++.h>
using namespace std;

/* Funtion to Calculate and Print Stock Span of Stock Prices  */
void stockSpan(int arr[], int size)
{
    int span[size];
    
    /* Calculate Stock Span */
    for(int i = 0; i < size; i++)
    {
        span[i] = 1;
        for(int j = i - 1; j >= 0; j--)
        {
            if(arr[i] >= arr[j])
            span[i]++;
            else
            break;
        }
    }
    
    /* Print Stock Span */
    for(int i = 0; i < size; i++)
    {
        cout<<span[i]<<" ";
    }
}


int  main()
{
    int arr[] = {67, 55, 100, 9, 11, 54};
    int size = sizeof(arr) / sizeof(arr[0]);
    stockSpan(arr,size);
}

OUTPUT:
1 1 3 1 2 3 
 
Time Complexity:
O(n2), where ‘n’ is the number of elements in the array.

Method 2: Stack-Based Approach

The stack-based approach is more time efficient than previous brute-force approach. It solves the problem in linear time complexity. The steps required to implement stock-based problem are as follows:

1. Create an empty array, named as span[], with same size as number of stock price day, which will store the span value of every stock price day. The span value of first day will always be 1, so assign span 1 to span[0]
2. Create an Empty Stack and push index 0 into it.
3. Iterate a loop from 1 to (<size) and for every stock price (arr[i]), pop elements from the stack while stack is not empty and arr[top_of_stack] is smaller than arr[i]. If stack becomes empty, then arr[i] is greater than all elements on left of it, Else, arr[i] is greater than elements after top of stack. Now, push ‘I’ into stack.

C++ Program to implement stock span problem is as follows:

/* C++ Problem to implement stock span problem */
#include<bits/stdc++.h>
using namespace std;

/* Funtion to Calculate and Print Stock Span of Stock Prices  */
void stockSpan(int arr[], int size)
{
    int span[size];
    /* Span Value of first stock price is always 1 */
    span[0] = 1;
    
    /* Create an Empty Stack and push index 0 into it. */
    stack<int> st;
    st.push(0);
    
    /* Calculate span value of rest of the stock prices */
    for(int i = 1; i < size; i++)
    {
        /*
           Pop Elements from Stack while stack is not empty and
           Top of stack is smaller than arr[i]
        */
        while(!st.empty() && arr[st.top()] <= arr[i])
        st.pop();
        
        /*
            If stack becomes empty, then arr[i] is greater than 
            all Elements on left of it. Else, arr[i] is greater than
            Elements after top of stack.
        */
        span[i] = (st.empty()) ? (i + 1) : (i - st.top());
        
        /* Push Current Element Index into stack */
        st.push(i);
    }
    
    /* Print Stock Span */
    for(int i = 0; i < size; i++)
    {
        cout<<span[i]<<" ";
    }
}


int  main()
{
    int arr[] = {67, 55, 100, 9, 11, 54};
    int size = sizeof(arr) / sizeof(arr[0]);
    stockSpan(arr,size);
}

OUTPUT:
1 1 3 1 2 3 

Related Posts:

1. Infix to Postfix Conversion
2. Infix to Prefix Conversion
3. Prefix to Infix Conversion
4. Prefix to Postfix Conversion
5. Postfix to Infix Conversion
6. Postfix to Prefix Conversion
7. Check whether given Parentheses String are Balanced Parentheses or Not.
8. Next Greater Element
9. Find Minimum number of bracket reversals required to make an expression balanced.
10. Implement Queue Using Two Stacks.
11. Merge Overlapping Intervals using Stacks
12. Implement Stack Using Linked List
13. Largest Rectangular Area in Histogram
14. Length of Longest Valid Substring
15. Reverse a String using Stack
16. Implement two stacks in a single array
17. Print Bracket Number
18. Next Greater Frequency Element
19. Remove Duplicate Nodes from an Unsorted Linked List.
20. Sort a Stack using Temporary Stack