Right View of Binary Tree
“Right View of Binary Tree” is a very popular interview problem based on Tree data structure, asked in many technical interviews. Here, we are given a binary tree and our task is to write a program to print the Right View of Binary Tree.
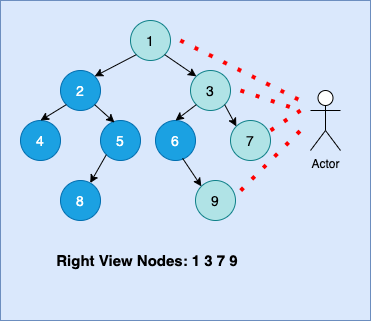
“Right View of Binary Tree” is defined as the nodes of the binary tree which are visible from right sides of the tree. These nodes are basically first nodes of every level of given binary tree, viewed from right side.
There can be multiple ways to print right view of binary tree. Some of them are:
- Modifying Preorder Traversal
- Modifying Level Order Traversal
Method 1: Modifying Preorder Traversal
Here, the idea is to traverse given tree in preorder manner and maintain maximum level visited so far.
The catch here is that in generic preorder traversal, we print root, then traverse left subtree and in last right subtree. But, here, instead of generic preorder traversal, firstly, we print the root, then traverse right subtree and in last traverse left subtree.
If current level is more than maximum level visited so far, then current node is first node of current level, then we print the current node and also update the maximum level visited so far to current level.
We perform all this operation in recursive manner.
C++ Program to Print Right View of Binary Tree is as follows:
/* C++ Program to Print Right View of Binary Tree */
#include<bits/stdc++.h>
using namespace std;
typedef struct Node
{
int data;
struct Node *left;
struct Node *right;
Node(int ele)
{
data = ele;
left = NULL;
right = NULL;
}
} Node;
/* Function to Print Right View of Binary Tree */
void rightViewPrint(Node *root, int curr_level, int &max_level)
{
/* Base Case */
if(root == NULL)
return;
/*
If current level is greater than maximum level visited so far,
then, print the current node and update the maximum level visited
so far to current level
*/
if(curr_level > max_level)
{
cout<<root -> data<<" ";
max_level = curr_level;
}
/* Recursively Traverse for Right and Left Subtree */
rightViewPrint(root -> right, curr_level+1, max_level);
rightViewPrint(root -> left, curr_level+1, max_level);
}
/* Function to Print Right View of binary Tree */
void rightView(Node *root)
{
int max_level = 0;
rightViewPrint(root, 1, max_level);
}
int main()
{
/* Creating a Binary tree and inserting some nodes in it */
Node *root = NULL;
root = new Node(1);
root -> left = new Node(2);
root -> right = new Node(3);
root -> left -> left = new Node(4);
root -> left -> right = new Node(5);
root -> right -> left = new Node(6);
root -> right -> right = new Node (7);
root -> left -> right -> left = new Node(8);
root -> right -> left -> right = new Node(9);
/* Calling function to print left view of binary tree */
cout<<"The Right View of Binary Tree is:\n";
rightView(root);
}
OUTPUT:
The Right View of Binary Tree is: 1 3 7 9
METHOD 2: Modifying Level Order Traversal
This is a simple modification of Level Order Traversal. Here, the idea is to print only first visited node of every level. This can be easily achieved by tracking the number of nodes at current level and first node of current level.
Here, again, instead of pushing left subtree node in queue, we will push right subtree node in queue.
C++ Program to Print Right View of Binary Tree is as follows:
/* C++ Program to Print Right View of Binary Tree */
#include<bits/stdc++.h>
using namespace std;
typedef struct Node
{
int data;
struct Node *left;
struct Node *right;
Node(int ele)
{
data = ele;
left = NULL;
right = NULL;
}
} Node;
/* Function to Print Right View of binary Tree */
void rightView(Node *root)
{
/* Base Case */
if(root == NULL)
return;
queue<Node*> que;
que.push(root);
while(!que.empty())
{
/* Keeping Track of number of nodes at current level */
int p = que.size();
for(int i = 1; i <= p; i++)
{
Node *temp = que.front();
/* If current node is first node of current level, print it */
if(i == 1)
{
cout<<temp->data<<" ";
}
/* Push Left and right Nodes*/
if(temp -> right)
que.push(temp -> right);
if(temp -> left)
que.push(temp -> left);
/* Pop out current node */
que.pop();
}
}
}
int main()
{
/* Creating a Binary tree and inserting some nodes in it */
Node *root = NULL;
root = new Node(1);
root -> left = new Node(2);
root -> right = new Node(3);
root -> left -> left = new Node(4);
root -> left -> right = new Node(5);
root -> right -> left = new Node(6);
root -> right -> right = new Node (7);
root -> left -> right -> left = new Node(8);
root -> right -> left -> right = new Node(9);
/* Calling function to print right view of binary tree */
cout<<"The Right View of Binary Tree is:\n";
rightView(root);
}
OUTPUT:
The Right View of Binary Tree is: 1 3 7 9
Related Posts:
- Left View of Binary Tree
- Compute Height of Binary Tree
- Inorder Tree Traversal Using Stack
- Preorder Tree Trasversal Using Stack
- Postorder Tree Traversal Using Stack
- Vertical Order Tree Traversal
- Top View of Binary Tree
- Bottom View of Binary Tree
- Delete Complete Binary Tree
- Check if two trees are mirror Trees of Each Other
- Convert Binary Tree to its Mirror Tree
- Check if Binary Tree is Symmetric or Not
- Print All Root to Leaf Paths in a Binary Tree
- Introduction to Tree Data Structure
- Binary Tree Traversals
- Print All Leaf Nodes of a Binary Tree
- Count Number of Nodes in a Binary Tree
- Print Alternate Levels of Binary Tree
- Maximum Width of Binary Tree
- Level Order Tree Traversal


